Demo-MAT4: Predictive Maintenance mit MATLAB
 Klassifikation von Ausfällen

Demo-MAT4 zeigt, wie eine Ausfall-Klassifikation im Rahmen eines Predictive Maintenance-Szenarios mit Hilfe des Entscheidungsbaum-Verfahrens der MATLAB Statistics and Machine Learning ToolBox durchgeführt wird. Wir verwenden denselben Automotive-Datensatz, der in allen Demos des Predictive Maintenance-Zyklus verwendet wird: eine csv-Datei automotive_data.csv mit 23 Merkmalen (Kühlmittel­temperatur, Drossel­klappen­stellung, ...) und einer Zielvariablen: Ausfall. Die Fragestellung lautet: "Bei welcher Kombination von Merkmalen tritt ein Ausfall ein?". Zunächst wird ein MATLAB Live Script erstellt, das die Schritte der Datenanalyse mit Hilfe der MATLAB-Funktionen erläutert, danach wird das Skript um eine interaktive Visualisierung für das Parametertuning des Modells erweitert.

  Motivation

In den Demonstratoren des Predictive Maintenance-Zyklus wird die Durchführung der Datenanalyse und Vorhersage im Rahmen der Vorausschauenden Wartung unter Verwendung verschiedener Datenanalyse-Tools durchgeführt: Python, R, RapidMiner. In dieser Demo verwenden wir die Funktionen der MATLAB Statistics and Machine Learning-Toolbox, sowie MATLAB Live Script für die Erstellung einer interaktiven Demo ein.

Warum Statistics and Machine Learning-Toolbox?

Die MATLAB Statistics and Machine Learning-Toolbox bietet eine Reihe von Funktionen und im allgemeinen Unterstützung für die üblichen Schritte des Überwachten und Unüberwachten Lernens: Datenvorbereitung, Trainingsphase und Modellevaluation, ebenso Algorithmen für Klassifikations-, Regressions- und Clustering-Probleme, siehe z.B. die Dokumentation der Funktionen für Klassifikation. Diese Toolbox enthält weiterhin Lern-Apps wie den ClassificationLearner , die das Erlernen des Datenanalyse-Prozesses unterstützen,

Warum MATLAB Live Script?

Ein MATLAB Live Script ist ein erweitertes MATLAB-Skript, wo die Benutzer-Eingaben, der Quellcode selbst, die Ausführung des Quellcodes und die Ausgabe der Ergebnisse (Grafiken, Werte der Berechnungen) in einem einzigen interaktiven Fenster angezeigt werden. Dies dient der Übersichtlichkeit und dem Nachvollziehen der Befehle und Funktionen. Welche Auswirkung eine Änderung im Quellcode hat, ist durch die Änderung der ausgegebenen Ergebnisse (Grafiken, Textausgaben, usw.) direkt und unmittelbar zu erkennen.

  Übersicht

Demo-MAT4 ist in 9 Abschnitte gegliedert. Zunächst wird der Automobil-Datensatz beschrieben und die Fragestellung, die wir mit unserer Datenanalyse beantworten wollen. Danach wird die Funktionsweise und Anwendung von Entscheidungsbäumen kurz vorgestellt, sowie die Erstellung des Live Scripts und Vorbereitung benötigter Bibliotheken. In den folgenden Abschnitten erfolgt die Erstellung eines Entscheidungsbaum-Vorhersagemodells mit Ermittlung von Performance-Kennzahlen, dessen Visualisierung als Text und Baum, sowie Durchführung einer Vorhersage an Testdaten.

• 1 Der Automotive-Datensatz

• 2 Die Fragestellung

• 3 Ablauf der Datenanalyse

• 4 Was ist ein Entscheidungsbaum?

• 5 Live-Script erstellen

• 6 Das Entscheidungsbaum-Vorhersagemodell

• 7 Vorhersage neuer Ausfälle

• 8 Weitere Performance-Kennzahlen: Accuracy, Precision, Recall mit Kreuzvalidierung

• 9 Interaktive Visualisierung

Live-Script herunterladen!

1 Der Automotive-Datensatz

Der Automobildatensatz ist eine csv-Datei und besteht aus insgesamt 140 Beobachtungen. Jede Beobachtung enthält den Vorhersagewert Ausfall, mit angenommenen Werten ja/nein, die Messungsnummer, und Sensorwerte zu insgesamt 22 Merkmalen. Die erhobenen Merkmalswerte stammen aus Temperatur- und Druckmessungen sowie Mengenangaben zum Kraftstoff und zu Abgasdämpfen, die an verschiedenen Stellen im Motor erfasst wurden. Für alle Merkmale liegen numerische Messungen vor. Als Trennzeichen für die Spalten wird das Semikolon verwendet.

2 Die Fragestellung

Uns interessiert, welche Merkmalskombinationen, d.h. welches Zusammenspiel der Sensorwerte, zu einem Ausfall des Motors führen. Die Frage, die der Entscheidungsbaum beantworten soll, lautet also: Welche Kombination von Merkmalen wird zu einem Ausfall führen? Werden alle Merkmale einen Einfluss auf den Ausfall haben und falls nein, mit welchem Gewicht werden welche Merkmale einen Ausfall bewirken?

3 Ablauf der Datenanalyse

Die Datenanalyse für die Predictive Maintenance läuft in fünf Schritten ab, wobei einige der Teilschritte je nach Daten und ausgewähltem Modell auch entfallen können. Z.B. ist bei einem Entscheidungsbaum-Modell keine Normalisierung der Daten erforderlich.

• Schritt 1. Datenvorbereitung: Der Datensatz wird in Trainings- und Testdaten zerlegt, die Zielvariable wird festgelegt und die Daten werden bereinigt, d.h. je nach Datenlage normalisiert und transformiert, bei fehlenden Werte interpoliert und durch Algorithmen werden Ausreißer erkannt und behandelt.
  

• Schritt 2. Modell definieren: Gemäß den Daten wird ein passendes Modell gewählt, dies kann ein Entscheidungsbaum-Modell für Klassifikation oder Regression sein, oder eine Nächste Nachbarn-Klassifikation, dies hängt von der Fragestellung ab.
  
• Schritt 3. Modell trainieren: Mit den Trainingsdaten wird das Modell erstellt, d.h die Parameter des Modells geschätzt, z.B. die Verzweigungen und Blätter eines Entscheidungsbaums oder die Parameter als Kleinste-Quadrate-Schätzer in einem Regressionsmodell.
• Schritt 4. Modell validieren: Das Modell wird auf die Testdaten angewandt um eine Vorhersage zu erhalten, der Vergleich der Vorhersagen mit den bekannten Werten der Zielvariablen liefert die Performance­-Kennzahlen, die den Testfehler beschreiben, und angeben wie gut ein Modell ist.
  
• Schritt 5. Modell verwenden: Liegt ein gutes Modell vor, dann werden durch Anwendung des Modells auf neue Beobachtungen, deren Werte der Zielvariablen unbekannt sind, Vorhersagen getätigt.

4 Was ist ein Entscheidungsbaum?

Ein Entscheidungsbaum ist ein Klassifikationsmodell, mit dessen Hilfe eine Ja-Nein Fragestellung beantwortet werden kann. In einem Predictive Maintenance-Szenario soll z.B. vorhergesagt werden, ob bei einer bestimmten Kombination von Messungen ein Ausfall eintritt oder nicht. Diese "Vorhersage" ist strenggenommen eine Klassifikation, also eine Funktion / Zuordnung, die die Merkmale einer Beobachtung auf die korrekten Zustände ("Ausfall" oder "Kein Ausfall") abbildet. Das Modell entsteht, indem die Datentabelle, die bei der Datenerhebung erfasst wurde, um eine Spalte ergänzt wird, die Zielvariable genannt wird und die die Bewertung des Zustands enthält. Für die Vergangenheits­daten ist die Bewertung bekannt, für neue Daten wird die Bewertung durch das Modell vorhergesagt.

Ein Entscheidungsbaum besteht aus einer Wurzel, Knoten und Blättern, wobei jeder Knoten eine Entscheidungsregel und jedes Blatt eine Antwort auf die Fragestellung darstellt. Um eine Klassifikation eines einzelnen Datenobjektes abzulesen, geht man vom Wurzelknoten entlang des Baumes abwärts. Bei jedem Knoten wird ein Merkmal abgefragt und eine Entscheidung über die Auswahl des folgenden Knoten getroffen. Dies wird so lange fortgesetzt, bis man ein Blatt erreicht. Das Blatt entspricht der Klassifikation.

Mini-Beispiel
Zur Veranschaulichung betrachten wir einen Datensatz mit Sensor-Messwerten mit nur zwei Merkmalen: Temperatur und Druck und einer Zielvariablen: Ausfall. Der Entscheidungsbaum für das Mini-Beispiel gibt eine Antwort auf die Frage, bei welcher Kombination von Werten für die Merkmale temp und druck das Gerät ausfallen wird.

Datensatz mit Zielvariable

id	temp	druck	ausfall
1	normal	hoch	nein
2	hoch	normal	nein
3	hoch	hoch	ja
4	hoch	normal	ja
5	hoch	hoch	?

Die Zeilen 1 bis 4 enthalten die Vergangen­heits­daten mit bekannter Bewertung der Ziel­variablen. Zeile 5 enthält eine neue Beobachtung, für die auf Basis des Entscheidungs­baums der Ausfall vorhergesagt wird.

Entscheidungsbaum

Wenn die Temperatur hoch und der Druck hoch ist, wird ein Ausfall vorhergesagt. Wenn die Temperatur normal ist, wird kein Ausfall eintreten.

Wie entsteht der Entscheidungsbaum?
Die genaue Form des Entscheidungsbaums entsteht durch den Trainingsprozess des überwachten Lernens. Die Input-Daten werden in Trainingsdaten und Testdaten unterteilt. Auf Basis der Trainingsdaten wird mittels eines passenden Algorithmus (CART, C4.5, ID3) der Entscheidungsbaum erstellt, dessen Güte mit Hilfe von Performance-Kennzahlen (z.B. Vertrauenswahrscheinlichkeit, Genauigkeit, Trefferquote) ermittelt wird. Der Trainingsprozess wird solange wiederholt, bis das Modell eine gewünschte Performance erreicht. Danach kann es für die Vorhersage auf neuen Datensätzen verwendet werden.

5 Live Script erstellen

Für die Datenvorbereitung, die Erstellung des Entscheidungsbaum-Vorhersagemodells und die Vorhersage selber wird ein Live Script verwendet.

Erstellen des Live Scripts

Ein MATLAB Live Skript wird entweder direkt über die Menüleiste des Live Editors erstellt ( New > Live Script), oder indem ein reguläres MATLAB-Skript (*.m-Datei) mit entsprechender Syntax Live Script geöffnet wird. Wir erstellen zunächst einen Entwurf, der die Struktur des Dokumentes entsprechend den Schritten der Datenanalyse enthält, d.h. wir fügen 5 Text-Zellen mit Überschriften ein, sowie 5 Codezellen, in die später der entsprechende MATLAB-Code eingefügt wird. Aus den Überschriften kann später auch ein Inhaltsverzeichnis für das Skript erstellt werden, dies macht eine spätere Veröffentlichung des Skripts als PDF ansprechender.

Das Skript wird durch Anklicken des Run-Buttons in der Menüleiste des Live Editors ausgeführt. Weiterhin können einzelne Code-Zellen ausgeführt werden, die Ausgabe erfolgt entweder in dem Ausgabefenster rechts oder inline.

Die Details der Verwendung von Live Scripts inkl. der speziellen Syntax sind im Abschnitt Live-Scripts verwenden beschrieben.

6 Das Entscheidungsbaum-Vorhersagemodell

Als Nächstes wird ein Entscheidungsbaum-Vorhersagemodell erstellt, an dem wir die korrekte Abfolge der Schritte (1. Daten einlesen, 2. Merkmale und Zielvariable extrahieren, 3. Vorhersagemodell erstellen, 4. Vorhersagemodell visualisieren, 5. Vorhersage durchführen) testen.

6-1 Datenvorbereitung: Daten einlesen

In der ersten Codezelle werden Daten, die in der csv-Datei automotive_data_train.csv gespeichert sind, mit Hilfe der Funktion readtable() in ein Tabellen-Objekt eingelesen, dabei können verschiedene Optionen als Name-Wert-Paare angegeben werden. Hier setzen wir die Option ReadVariableNames auf den Wert true, um die Spaltenüberschriften mit zu lesen, und die Option VariableNamingRule mit dem Wert 'preserve', um die genauen Spaltenüberschriften beizubehalten.

Danach zeigen wir mit head die ersten 6 Zeilen der Tabelle data an und geben mit summary eine statistische Übersicht der Variablen aus.

% Daten einlesen
data = readtable('automotive_data_train.csv', ...
    'ReadVariableNames', true, ...
    'VariableNamingRule', 'preserve'); 
% Erste 6 Zeilen anzeigen
disp(head(data))
% Statistische Übersicht der Variablen
summary(data)

Erläuterung:
Die Ausgabe zeigt die ersten 6 Zeilen der Tabelle, sowie die statistische Übersicht der Variablen.

Zielvariable und Merkmale

6-2 Datenvorbereitung: Merkmale und Zielvariable extrahieren

In der zweiten Codezelle werden die Merkmale und die Zielvariable aus der Tabelle data extrahiert.

% Merkmale: Variablen 3 bis 23
X_train = data(1:end, 3:23); 
% Zielvariable: Ausfall 2te Spalte)
Y_train = data(1:end,2);
disp("Zielvariable und Merkmale (Auszug):");
disp([Y_train(1:5, 1), X_train(1:5, 1:3)]);
% Name der Variablen / Merkmale
disp("Variablen-Namen:");
disp(X_train.Properties.VariableNames');

Erläuterung:
Die Merkmale, die wir für das Training des Modells heranziehen, sind alle Spalten außer Spalte 1 (Messungsnummer) und Spalte 2 (Ausfall), daher extrahieren wir die Spalten 2 bis 23 in die Tabelle X_Train. Die Zielvariable (Spalte 2, Ausfall) wird in die Tabelle Y_Train extrahiert.

Für die Kontrolle des Ergebnisses (und als Übung) führen wir die extrahierten Daten in eine neue Tabelle zusammen und geben auch die Namen der Variablen aus.

Zielvariable und Merkmale

6-3 Vorhersagemodell erstellen

Das Vorhersagemodell für die Trainingsdaten (X_train, Y_train) wird mit Hilfe der Funktion fitctree() erstellt. Diese Funktion verwendet standardmäßig eine optimierte Version des CART-Algorithmus und gibt ein Objekt der Klasse ClassificationTree zurück. Diese Klasse fasst alle Eigenschaften und Methoden eines Entscheidungsbaum-Modells zusammen. Beim Erstellen des Modells mit Hilfe der Funktion werden verschiedene Konfigurationsparameter festgelegt, die steuern, wie genau der Entscheidungsbaum aufgebaut wird, die wichtigsten sind: SplitCriterion, PredictorSelection, MinParentSize, MaxNumSplits.

% Parameterwahl
min_parent_size = 10;
max_num_splits = 14;
% Erstellung des Modells
model = fitctree(X_train, Y_train,'SplitCriterion','deviance',...
'MinParentSize', min_parent_size, ...
'MaxNumSplits', max_num_splits,...
'MinLeafSize', 2, ...
'Reproducible', true);
disp('== Modell trainieren ==')
whos model
model
disp('== Parameter == ');disp(model.ModelParameters);

Modell-Details

Modell-Parameter

Erläuterung der wichtigsten Parameter

• SplitCriterion: legt fest, welche Funktion verwendet wird, um die Güte einer Aufteilung (engl. Split) an einem Knoten zu messen. Als Kriterium kann entweder "gdi" (Gini-Index), "twoing" oder "deviance" (Entropie bzw. Informationsgehalt) verwendet werden. Wir wählen das Kriterium "deviance".
• MinParentSize: bestimmt die minimal erforderliche Anzahl der Beobachtungen für die Aufteilung eines Knotens. Wir setzen MinParentSize = 10, d.h. ein Knoten wird nur aufgeteilt, wenn er mindestens 10 Beobachtungen enthält.
• MaxNumSplits: bestimmt die maximale Anzahl an Verzweigungen, die ein Baum enthalten kann, Defaultwert ist die Größe des Trainingsdatensatzes minus 1. Dieser Parameter kann verwendet werden, um die Tiefe des Baums zu beeinflussen.
• MaxLeafSize: maximale Anzahl der Beobachtungen in einem Knoten, Defaultwert ist 1. Falls dieser Wert zu klein ist, wird der Baum zu detailliert und verzweigt.

6-4 Visualisierung des Entscheidungsbaums

Der Entscheidungsbaum wird mit Hilfe der Funktion view entweder in Text-Form oder in Baum-Form visualisiert. Die Grafikausgabe des Baums öffnet den Classification Tree Viewer, eine Benutzeroberfläche, in der noch weitere Einstellungen an dem Baum-Modell vorgenommen werden können.

view(model,'mode','graph') 
view(model) 

Grafikausgabe des Baums

Textausgabe des Baums

6-5 Performance bewerten

In diesem Abschnitt bewerten wir das zuvor erstellte Modell mit Hilfe unterschiedlicher Kennzahlen und der Methode der Kreuzvalidierung, die in dem elab2go-Artikel Datenanalyse - Kennzahlen genauer beschrieben wird.

Im folgenden ermitteln wir zunächst die Performance-Kennzahl Accuracy über die Kreuzvalidierung mittels der MATLAB-Funktion crossval, kFoldPredict und kFoldLoss und bewerten damit die Güte des Vorhersagemodells. Die Funktion crossval erstellt ein neues Datenmodell durch die Methode der Kreuzvalidierung: der Datensatz wird in 10 Partitionen unterteilt und das Modell auf diesen trainiert, wobei der jeweils verbleibende Rest einer Partition als Testdatensatz verwendet wird.

% Kreuzvalidierung (1) mit Toolbox-Funktionen
kFold = 10; % Anzahl Partitionen
partitionedModel = crossval(model, 'KFold', 10);
% Berechne Vorhersagen
[valPredictions, valScores] = kfoldPredict(partitionedModel);
% Berechne Accuracy
valAccuracy = 1 - kfoldLoss(partitionedModel, 'LossFun', 'ClassifError');
T = array2table([valAccuracy], 'VariableNames', {'Accuracy'});
disp(T);

Erläuterung:
Mit Hilfe der Funktion crossval wird zunächst ein optimiertes Modell partitionedModel erstellt, dies wird dann für die Vorhersage mit Hilfe der Funktion kfoldPredict genutzt, und zuletzt wird die Vertrauenswahrscheinlichkeit für dies Modell aus der errechneten Verlustfunktion berechnet.

Vertrauenswahrscheinlichkeit

7 Vorhersage neuer Ausfälle

Nachdem ein Entscheidungsbaum-Modell erstellt wurde, kann es zur Vorhersage des Ausfalls auf neuen Datensätzen verwendet werden. Zunächst wird ein neuer Test-Datensatz (hier: automotive_data_test.csv, ein kleiner Datensatz mit nur 4 Zeilen) mit der Funktion readtable in ein Tabellen-Objekt X_test eingelesen. Danach wird die Funktion predict aufgerufen, wir übergeben ihr als Parameter das zuvor erstellte Modell model sowie die Testdaten X_test, und sie gibt die Vorhersage Y_pred zurück.

% Testdaten einlesen
data_test = readtable('automotive_data_test.csv', ...
    'ReadVariableNames',true, ...
    'VariableNamingRule', 'preserve');
X_test = data_test(1:end,3:23); % extrahiere Merkmale 
% Vorhersage mittels Baum
Y_pred = predict(model, X_test);
% Ausgabe
disp('Testdaten:')
disp(data_test); 
disp('Die Vorhersage für die Testdaten lautet:')
disp([data_test(:, 1), Y_pred, X_test]);

Erläuterung:
Die Spalte "Ausfall" in den Testdaten enthält keine Werte, diese sollen hier vorausgesagt werden. Nach der Durchführung der Vorhersage (eigentlich: Klassifikation) mittels predict stehen die Ausfall-Werte in der 4x1 Zelle Y_pred. Für eine anschauliche Ausgabe fügen wir die Spalte mit den Messungsnummern (data_test(:, 1)), die Spalte mit den Ausfällen (Y_Pred) und die Merkmale (X_Test) wieder in eine einzige Tabelle zusammen.

Vorhersage des Ausfalls für die Testdaten

8 Weitere Performance-Kennzahlen

In einem Predictive Maintenance-Szenario entstehen dem Unternehmen einerseits Kosten, falls ein Ausfall nicht als solcher erkannt wird, dies würde durch die Kennzahl Trefferquote / Recall gemessen werden. Es entstehen aber auch Kosten, falls fälschlicherweise ein Ausfall vorhergesagt und die Produktion unterbrochen wird, dies würde durch die Kennzahl Genauigkeit / Precision gemessen werden. D.h. die Kennzahlen Precision und Recall sind ebenso wichtig, wie die Vertrauenswahrscheinlichkeit.

Wir entwickeln zunächst eine Funktion cross_validation(X_train, Y_train, param, k), die auf den Trainingsdaten eine Kreuzvalidierung durchführt und eine Tabelle mit den Kennzahlen Accuracy, Recall, Precision zurückgibt.

function T = cross_validation(X_train, Y_train, param, k)
index = cvpartition(1:size(Y_train, 1),'k', k);
m_kenn = zeros(index.NumTestSets, 3);
for i = 1:index.NumTestSets % Kreuzvalidierung
    trIdx = index.training(i);
    teIdx = index.test(i);
    treeCV = fitctree(X_train(trIdx,:), Y_train(trIdx,:), ...
        'SplitCriterion','deviance', 'MinParentSize', param(1), ...
        'MaxNumSplits', param(2), 'MinLeafSize', param(3), ...
        'Reproducible', true);
    predictCV = predict(treeCV, X_train(teIdx,:));    
    actual = strcmp(Y_train{teIdx,:}, 'ja');
    predictCV = strcmp(predictCV, 'ja');
    Cf = cfmatrix2(actual, predictCV, [0,1], 0, 0); 
    m_kenn(i,1) = Cf{1}(1,2); % Precision
    m_kenn(i,2) = Cf{1}(2,2); % Recall
    m_kenn(i,3) = Cf{2}; % Accuracy
end
kenn = sum(m_kenn(:,:))/index.NumTestSets;
T = array2table(kenn, 'VariableNames', {'Accuracy', 'Recall', 'Precision'});
end

Erläuterung des Codes:
In der for-Schleife (ab Zeile 6) wird die Kreuzvaliderung durchgeführt, wobei X_train(index.training(i),:) als Trainings- und X_train(index.test(i),:) als Testdatensatz für den i-ten Durchlauf verwendet wird. Für jeweils den i-ten Teildatensatz X_train(trIdx,:) wird das Vorhersage-Modell treeCV mit Hilfe der "fitctree"-Funktion erstellt, dieses wird zusammen mit dem Testdatensatz der "predict"-Funktion übergeben und die Vorhersagen werden danach in der "cfmatrix2"-Funktion mit den tatsächlichen Werten für den Ausfall der Testdaten verglichen. Zuletzt werden die summierten Kennzahlen der einzelnen Kreuzvalidierungs-Durchläufe durch die Anzahl der gesamten Durchläufe NumTestSets geteilt, um mittlere Kennzahlen zu erhalten. Die Teilergebnisse werden in einer Matrix gespeichert und als Tabelle T zurückgegeben.

% Parameter
min_parent_size=10; max_num_splits=20; min_leaf_size=1;
param = [min_parent_size, max_num_splits, min_leaf_size];
paramTable = array2table(param, 'VariableNames', ...
{'MinParentSize', 'MaxNumSplits', 'MinLeafSize'});
% Anzahl Partitionen
k = 10; 
% Berechne Kennzahlen mit Funktion cross_validation
T = cross_validation(X_train, Y_train, param, k);
disp('Modell-Parameter:');
paramTable
disp('Performance-Kennzahlen:');
T

Erläuterung:
Um die Funktion cross_validation zu testen, werden zunächst die Hyperparameter min_parent_size, max_num_splits und min_leaf_size für das Modell festgelegt und in einem Array param gespeichert (Zeile 1 bis 5), sowie die Anzahl der Partitionen für die Kreuzvalidierung auf k = 10 festgelegt. In Zeile 10 rufen wir die Funktion mit den zuvor definierten Parametern auf und bestimmen damit die Kennzahlen-Tabelle T, die wir anschließend ausgeben.

Performance-Kennzahlen

9 Interaktive Visualisierung

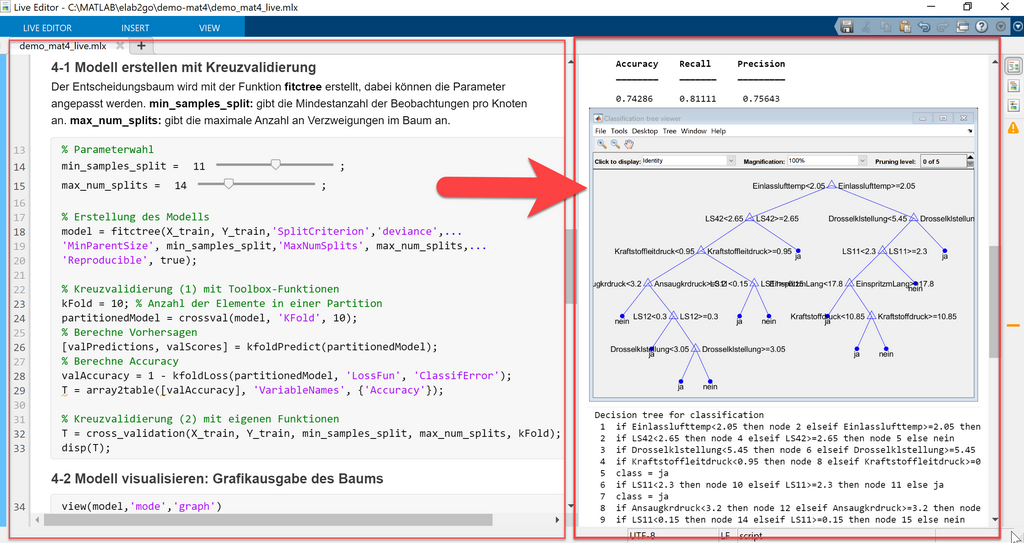
Nachdem die grundlegenden Funktionen der Klassifikation mit Entscheidungsbäumen getestet wurden, erstellen wir als Nächstes eine interaktive Visualisierung des Entscheidungsbaums, mit dem Ziel, die Wirkung der unterschiedlichen Parameter auf die Performance des Modells zu testen.

Dafür verwenden wir im Live Script für jeden der Hyperparameter ein Slider-Control, und weisen ihm als Aktion die Ausführung der aktuellen Codezelle zu, die den Code für die Erstellung des Modells, die Berechnung der Performance-Kennzahlen, sovie Visualisierung des Modells als Text und Baum enthält.

MATLAB-Code

Ausgabe

Autoren, Tools und Quellen